Represented while preserving its original size. By connecting the area of a circle to the area of a parallelogram, students can establish meaningful connections to their prior study of area of parallelograms in 6.G.1. The learning map section for this sequence of activities includes prerequisite knowledge of length, perimeter, and the ability to represent and solve equations. Building on an understanding of length, students can learn to explain diameter and radius.
An understanding of perimeter provides the foundation for students to explain circumference. This area and circumference of circles bingo game is full of word problems. Students have to find area and circumference with different measurements and sometimes in terms of pi. Some of the questions are a little bit easier where they just have to find the diameter or radius. Each question is based off of a picture, like a guy holding 10 boxes of pizza, a dog catching a Frisbee, or a girl counting coins.
I like to use this game for whole class review at the end of the unit. Try this game you'll have your students practicing in a fun and engaging way. Ask students what the base of the parallelogram would be related to the original circle. Questions could include, "Can you describe where the circumference of the circle falls on the decomposed circle? " and, "If the whole circumference is represented somewhere in this image, what fraction of the circumference falls here ? " Note that as the sectors get smaller, the shape gets closer and closer to a rectangle.
Remind students what the formula is for area of a parallelogram, and use this to derive the formula for the area of a circle. An example process is shown following this paragraph. We'll teach you the key circumference formulas you need to figure out the circumference of a circle when you know either the diameter or radius. In this article about the circumference of a circle, we saw the definition, formulas, and ways to find out the circumference of a circle, along with several solved examples. The learning outcome of this article is that one can calculate the circumference of circular objects and circular paths.
Sometimes I hear teachers talk about whether they should teach area first or circumference first. Personally, I believe you should teach them together and that student really need to understand the differences. The following list of activities will give your students lots of opportunities to practice working with and solving problems related to finding the area and circumference of circles. Area and circumference of a circle often gives our students their first taste of geometry during the year. Also, it seems like students see formulas for the first time when learning this topic. Usually, they don't come to us understanding how to plug values into formulas.
That means that we have to teach the idea of using formulas to them as well as how to find the area and circumference of a circle. Even though that can feel daunting, though, the great thing about circles and geometry is that they lend themselves to application pretty easily. We definitely have the opportunity to let students see area and circumference in a hands-on way. This post is full of engaging, fun area and circumference activities for secondary math students. Also, you can have students share their plates with other people and get some math talk going. At the end of the activity they can hang their creations on the wall and do a gallery walk to look at other people's plates.
The blog post where I got this idea used this activity for Pi Day and has them decorate the plates like a pie. I think it can be used during Pi Day or any time of year when you have your unit on area and circumference of circles. Acircleis a closed round shape with all the points equidistant from a fixed point known as the centre. The circle's circumference is measured in length units such asmetresandcentimetres.
Similarly, we come across more circular shapes in our everyday life like a dinner plate, Ferris wheel, the dial of a clock, cricket ground, candy, steering wheel, etc. Two formulas are used to find circumference, C, depending on the given information. Both circumference formulas use the irrational number Pi, which is symbolized with the Greek letter, π.
Pi is a mathematical constant and it is also the ratio of the circumference of a circle to the diameter. Use this practice quiz to ensure that your students have a complete understanding of how to calculate the circumference of a circle given its radius or diameter. This online lesson from onlinemathlearning.com provides a good explanation about how to use either radius or diameter to calculate the circumference of a circle. In this lesson, we will investigate how to calculate the circumference of a circle. We will explore the formula used for this calculation, and practise finding the circumference from a given radius or diameter. OpenUp is an amazing resource for complete math lessons that allow students to learn through hands-on activities.
Circumference Of A Circle Formula Proof By engaging with this lesson, students will be able to describe the relationship between circumference and diameter of any circle and explain what π means. When the formula for calculating the circumference of a circle is used, the circle's radius is considered. As a result, the radius or diameter value must be known to calculate the circle's perimeter or circumference.
Be careful not to overlook the beginning of this lesson. The lesson opens with the definition of a polygon. Sometimes polygons are oddly shaped; they are not usually your typical rectangles and squares.
Within modern architecture, there is a good possibility that you may work in office spaces that are oddly shaped in design. You might be asked to work in or set up work spaces in offices that have no right angles or possibly no straight walls. This module discusses perimeter and circumference of geometric figures. By the end of this lesson, you should be familiar with the definition of polygon, diameter and radius of a circle, and how to calculate the perimeter and circumference of a circle.
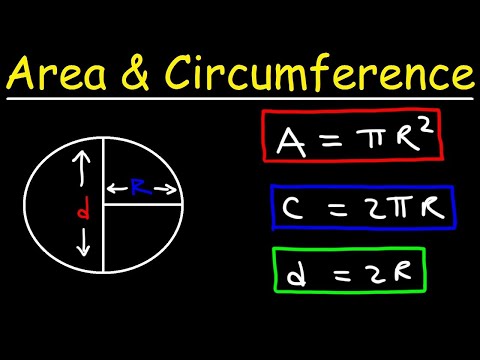
The radius, the diameter, and the circumference are the three defining aspects of every circle. Given the radius or diameter and pi you can calculate the circumference. The diameter is the distance from one side of the circle to the other at its widest points. The diameter will always pass through the center of the circle.
You can also think of the radius as the distance between the center of the circle and its edge. This Study Jams resource is great for introducing students to concepts related to measuring circles by building upon their current knowledge of measuring distance around objects. Students are guided through the process of finding the circumference of a circle using pi. They'll also learn how to use pi(π) when dealing with circle calculations. When they finish the activity I would have them write a reflection of their experience using this tool. This is a great opportunity to find out what students understand about finding the area and circumference of circles.
In addition, you can see some misconceptions, as well. For this activity students color in the area and then use wikisticks or yarn to measure the circumference. They approximate the area using squares that are on the paper. By counting the inch squares, students actually see why area is measured in square inches.
This gives them a chance to really see what is happening when we talk about area and circumference. Then you always have an experience to lead them back to when they get that look on their face like, "Which one is area and which one is circumference, again? " You can read more in this step by step guide of how this activity walks students through this discovery process in this post. Although the circumference of a circle is the length of its boundary, it cannot be calculated with the help of a ruler like it is usually done for other polygons.
Therefore, to calculate the circumference of a circle, we apply a formula that uses the radius or the diameter of the circle and the value of Pi (π). The distance from the centre to the outer line of the circle is called a radius. It is the most important quantity of the circle based on which formulas for the area and circumference of the circle are derived. Twice the radius of a circle is called the diameter of the circle. The diameter cuts the circle into two equal parts, which is called a semi-circle. This lesson has provided you with lots of information the circumference of circles and a way to find any the measure of any one part if you have another measurement.
Along the way, you also learned a little geography and history, which may also come in handy to you. Ask students what they think would happen if they could cut the circle into an infinite number of sectors and arrange them in a similar fashion . Ask students what they think is true about the area of this figure compared to the area of the original circle . Draw the radius on one of the sectors as shown in the following image . Ask students what measurement this would be, approximately, in a parallelogram . If students struggle to answer, you could draw in a parallelogram as shown in the following image to scaffold the question.
The given material would need to be purchased. In the preceding example, there is an opportunity to ask students how many sections of fence they would have to purchase if it is sold in 6-foot sections. This leads to a discussion that in real-world situations, rounding up is necessary to ensure there is enough material to complete the job.
Require students to practice Questions 8–13 to find either circumference, radius, or diameter in realworld and mathematical problems. PRIMARY ACTIVITY Students will measure circular objects and create definitions to support their understanding of diameter, radius, circumference, and pi. You can think of it as the line that defines the shape. For shapes made of straight edges this line is called theperimeter but for circles this defining line is called the circumference. Help students discover the relationship between diameter and circumference with this interactive.
Provides great support for visual learners who need to envision the relationship between a circle's circumference and diameter in a different way. Set the diameter, unravel the circle and then drag the diameter onto the unraveled circumference. These activities can be used practice or review and will get your students engaged in practicing finding the area and circumference of a circle.
My challenge to you is to just try one thing. I find that when I try something new it gets me more involved in the teaching. The students will appreciate it because they get tired of doing the same things over and over. So, good luck in your teaching or reviewing of this topic. Just remember, great teachers are always refining their craft. I hope you've found some activities or tools here that will help you take your area and circumference unit to the next level.
My kids love to review using whole class games. Jeopardy is one of the games we play periodically. This game of Jeopardy gives students practice in finding the radius, finding the diameter, and finding area and circumference.
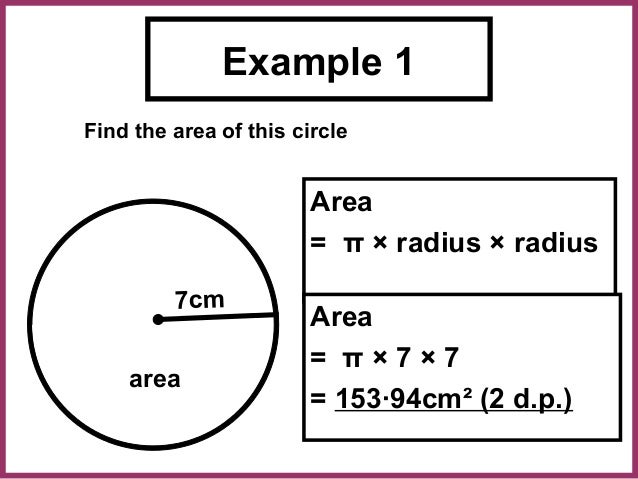
When I play all students write their answers on a whiteboard or SmartPal. I find that if everyone has to write down the answers then they are more accountable. This activity is great for the day you introduce the topic or the day before the test. Once again in this example, we're given the radius of the circle. Although it's not a clean number like our previous example, but we can still simply plug the number directly into the formula like what we did above.
Be aware of the units that this circle's radius is given in and remember to give your final answer in the same unit. In this question, we find that the circumference is equalled to 53.41m. Pi is a constant value used for the measurement of the area and circumference of a circle or other circular figures.
The symbol of pi is π and its numeric value is equal to 22/7 or 3.14. Further, these numeric values are used based on the context of the equation. The perimeter of a circle is the same as the circumference of a circle. It is the total length of the outer boundary of the circle. The perimeter or circumference of a circle is the product of the constant 'pi' and the diameter of the circle. It is expressed in linear units like m, inch, cms, feet.
The perimeter and area of triangles, quadrilaterals , circles, arcs, sectors and composite shapes can all be calculated using relevant formulae. Measurements usually have units to tell us what the numbers are measuring. They can also be centimeters, meters, or kilometers. The important thing when measuring circumference is to use consistent units. That means if the diameter is in yards, your circumference will also be in yards. If the diameter is in inches, the circumference will also be in inches.
When you write the circumference, make sure you write the unit with the number. Circumference of the circle or perimeter of the circle is the measurement of the boundary of the circle. Whereas the area of circle defines the region occupied by it. If we open a circle and make a straight line out of it, then its length is the circumference. It is usually measured in units, such as cm or unit m. A circle known to us is described as a form where all the locations are equidistant from a point at the centre.
The definition of the circumference of a circle in mathematics is the distance around the circle. It is the 1D linear estimation of the boundary across any two-dimensional circular surface. The circumference's ratio to its diameter is fixed in any circle drawn with any radius. This ratio is represented using the Greek letter .
If we take any circular objects around us and find the ratio of the circumference to its diameter, it is always a fixed constant (\pi ). We come across many shapes in our daily lives, but the circle's most commonly used shape. The length of their boundary is the circumference of that coin. The circumference of any object in mathematics specifies the route or border that surrounds the object. In other words, Thecircumference of a circleis the circle's perimeter. As stated before, the perimeter or circumference of a circle is the distance around a circle or any circular shape.